Real Numbers

Question 1.
Use Euclid’s division algorithm to find the HCF of

i) 900 and 270

Answer:
900 = 270 × 3 + 90
270 = 90 × 3 + 0
∴ HCF = 90

ii) 196 and 38220

Answer:
38220 = 196 × 195 + 0
∴ 196 is the HCF of 196 and 38220.

iii) 1651 and 2032

Answer:
2032 = 1651 × 1 + 381
1651 = 381 × 4 + 127
381 = 127 × 3 + 0
∴ HCF = 127

Question 2.
Use Euclid division lemma to show that any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integers.

Answer:
Let ‘a’ be an odd positive integer.
Let us now apply division algorithm with a and b = 6.
∵ 0 ≤ r < 6, the possible remainders are 0, 1, 2, 3, 4 and 5.
i.e., ’a’ can be 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4 or 6q + 5, where q is the quotient.
But ‘a’ is taken as an odd number.
∴ a can’t be 6q or 6q + 2 or 6q + 4.
∴ Any odd integer is of the form 6q + 1, 6q + 3 or 6q + 5.

Question 3.
Use Euclid’s division lemma to show that the square of any positive integer is of the form 3p, 3p + 1.

Answer:
Let ‘a’ be the square of an integer.
Applying Euclid’s division lemma with a and b = 3
Since 0 ≤ r < 3, the possible remainders are 0, 1, and 2.
∴ a = 3q (or) 3q + 1 (or) 3q + 2
∴ Any square number is of the form 3q, 3q + 1 or 3q + 2, where q is the quotient.
(or)
Let ‘a’ be a positive integer
So it can be expressed as a = bq + r (from Euclideans lemma)
now consider b = 3 then possible values of ‘r’ are ‘0’ or ‘1’ or 2.
then a = 3q + 0 = 3q (or) 3q + 1 or 3q + 2 now square of given positive integer (a²) will be
Case - I: a²- (3q)²= 9q²=3(3q²) = 3p (p = 3q²)
Case-II: a²= (3q + l)²= 9q²+ 6q+ 1
= 3[3q²+ 2q] + 1 = 3p+l (Where p = 3q²+ 2q) or
Case - III: a²= (3q + 2)²= 9q²+ 12q + 4 = 9q²+ 12q + 3 + 1
= 3[3q²+ 4q + 1] + 1
= 3p + 1 (where ‘p’ = 3q²+ 4q + 1)
So from above cases 1, 2, 3 it is clear that square of a positive integer (a) is of the form 3p or 3p + 1
Hence proved.

Question 4.
Use Euclid’s division lemma to show that the cube of a positive integer is of the form 9m, 9m + 1 or 9m + 8.
(OR)
Show that the cube of any positive integer is of form 9m or 9m + 1 or 9m + 8, where m is an integer.

Answer:
Let ‘a’ be positive integer. Then from Euclidean lemma a = bq + r;
now consider b = 9 then 0 ≤ r < 9, it means remainder will be 0, or 1, 2, 3, 4, 5, 6, 7, or 8
So a = bq + r
⇒ a = 9q + r (for b = 9)
now cube of a = a³+ (9q + r)³
= (9q)³+ 3.(9q)³r + 3. 9q.r + r³
= 9³q³+ 3.9²(q²r) + 3.9(q.r) + r³
= 9[9².q³+ 3.9.q²r + 3.q.r] + r³
a³= 9m + r³(where ‘m’ = 9²q³+ 3.9.q2r + 3.q.r)
if r = 0 ⇒ r³= 0 then a³= 9m + 0 = 9m
and for r = 1 ⇒ r³= l³then a³= 9m + 1
and for r = 2 ⇒ r³= 2³then a³= 9m + 8
for r = 3 ⇒ r³, = 3³⇒ a³= 9m + 27 = 9(m) where m = (9m +3)
for r = 4 ⇒ r³= 4³⇒ a³= 9m + 64 = (9m + 63) + 1 = 9m + 1
for r = 5 ⇒ r³= 125 ⇒ a³= 9m + 125 = (9m + 117) + 8 = 9m + 8
for r = 6 ⇒ r³- 216 ⇒ a³= 9m + 216 = 9m + 9(24) = 9m
for r = 7 ⇒ r³= 243
⇒ a³= 9m + 9(27) = 9m
for r = 8 ⇒ r³= 512
⇒ a³= 9m + 9(56) + 8 = 9m + 8
So from the above it is clear that a³is either in the form of 9m or 9m + 1 or 9m + 8.
Hence proved.

Question 5.
Show that one and only one out of n, n + 2 or n + 4 is divisible by 3, where n is any positive integer.
(Or)
Show that one and only one out of a, a + 2 and a + 4 is divisible by 3 where ‘a’ is any positive integer.

Answer:
Let ‘n’ be any positive integer.
Then from Euclidean’s lemma n = bq + r (now consider b = 3)
⇒ n = 3q + r (here 0 ≤ r < 3) which means the possible values of ‘r’ = 0 or 1 or 2
Now consider r = 0 then ‘n’ = 3q (divisible by 3)
and n + 2 = 3q + 2 (not divisible by 3)
n + 4 = 3q + 4 (not divisible by 3)
Case - II: For r = 1
n = 3q + 1 (not divisible by 3)
n + 2 = 3q + 1 + 2 = 3q + 3 = 3(q + l) divisible by 3
n + 4 = 3q + 1 + 4 = 3q + 5 not divisible by 3
Case – III: For r = 2,
n = 3q + 2 not divisible by 3
n + 2 = 3q + 2 + 2 = 3q + 4, not divisible by 3
n + 4 = 3q + 2 + 4 = 3q + 6 = 3(q + 2) divisible by 3
So in all above three cases we observe, only one of either (n) or (n + 1) or (n + 4) is divisible by 3.
Hence proved.

Question 1.
Express each of the following numbers as a product of its prime factors.

• i) 140
• ii) 156
• iii) 3825
• iv) 5005
• v) 7429

Answer:
i) 140

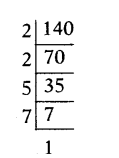
∴ 140 = 2 × 2 × 5 × 7 = 2² × 5 × 7

ii) 156

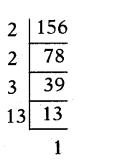
∴156 = 2 × 2 × 3 × 13 = 2² × 3 × 13

iii) 3825

∴ 3825 = 3 × 3 × 5 × 5 × 17 = 3² × 5² × 17

iv) 5005

∴ 5005 = 5 × 7 × 11 × 13

v) 7429

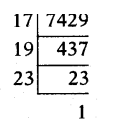
∴7429 = 17 × 19 × 23

Question 2.
Find the L.C.M and H.C.F of the following integers by the prime factorization method.

• i) 12, 15 and 21
• ii) 17, 23 and 29
• iii) 8, 9 and 25
• iv) 72 and 108
• v) 306 and 657

Answer:
i) 12, 15 and 21
12 = 2 × 2 × 3 = 22 × 3
15 = 3 × 5
21 = 3 × 7
L.C.M = 2²× 3 × 5 × 7 = 420
H.C.F = 3

ii) 17, 23 and 29
The given numbers 17, 23 and 29 are all primes.
L.C.M = their product
= 17 × 23 × 29 = 11339
∴ H.C.F = 1

iii) 8, 9 and 25
8 = 2 × 2 × 2 = 2³
9 = 3 × 3 = 3²
25 = 5 × 5 = 5²
L.C.M = 2³× 3²× 5²= 1800
(or)
8, 9 and 25 are relatively prime, therefore L.C.M is equal to their product,
(i.e.,) L.C.M = 8 × 9 × 25 = 1800
H.C.F = 1

iv) 72 and 108

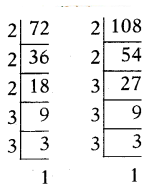
72 = 2³× 3²
108 = 2²× 3³
L.C.M = 2³× 3³= 8 × 27 = 216
H.C.F = 2²× 3²= 4 × 9 = 36

v) 306 and 657

306 = 2 × 3²× 17
657 = 32 × 73
L.C.M = 2 × 3²× 17 × 73 = 22338
H.C.F = 3²= 9

Question 3.
Check whether 6ⁿcan end with the digit ‘0’ for any natural number n.

Answer:
Given number = 6ⁿ= (2 × 3)ⁿ
The prime factors here are 2 and 3 only.
To be end with 0; 6ⁿshould have a prime factor 5 and also 2.
So, 6ⁿcan’t end with zero.

Question 4.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.

Answer:
Given numbers are 7 × 11 × 13
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
⇒ 13(7 × 11 + 1) and
5(7 × 6 × 4 × 3 × 2 × 1 + 1)
⇒ 13 K and 5 L, where K = 78 and L = 7 × 6 × 4 × 3 × 2 × 1 + 1 = 1009
As the given numbers can be written as product of two numbers, they are composite.

Question 5.
How will you show that (17 × 11 × 2) + (17 × 11 × 5) is a composite number? Explain.
Answer:
(17 × 11 × 2) + (17 × 11 × 5)
= (17 × 11) (2 + 5)
= (17 × 11) (7)
= 187 × 7
Now the given expression is written as a product of two integers and hence it is a composite number.

Question 6.
What is the last digit of 6100?

Answer:

We know that
6¹= 6
6²= 36
6³= 216
6⁴= 1296
6⁵= 7776
We see that 6ⁿfor any positive integer n ends is 6.
i.e., unit digit is always 6.
∴ Unit digit of 6¹⁰⁰is 6.

Question 1.
Write the following rational numbers in their decimal form and also state which are terminating and which have non-terminating repeating decimals.

i)3/8
ii)229/400
iii)4 1/5
iv)2/11
v)81/25

Answer:
i)3/8

[!! Denominator 8 = 2³, consists of only 2’s. Hence a terminating decimal.]
∴3/8= 0.375 is a terminating decimal.

ii) 229/400

[!! Denominator 400 = 2⁴ × 5² = 2ⁿ × 5^m. Hence a terminating decimal.]
∴ 229400 = 0.5725 is a terminating decimal.

iii) 4 1/5
4 1/5 = 4 + 1/5

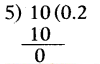
[!! Denominator is 5. Hence a terminating decimal.]
∴ 415 = 4.2 is a terminating decimal.

iv) 2/11

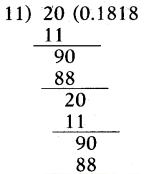
Question 2.
Without performing division, state whether the following rational numbers will have a terminating decimal form or a non-terminating, repeating decimal form.

• i)13/3125
• ii)11/12
• iii)64/455
• iv)15/1600
• v)29/343
• vi)23/2³5²
• vii)129/2².5⁷.7⁵
• viii)9/15
• iX)36/100
• X)77/210

Answer:
i)13/3125
Note: We check whether the denominator is of the form 2ⁿ. 5^mor not? If yes, the rational number can be expressed as a terminating decimal. If not, it can’t be expressed as a terminating decimal.

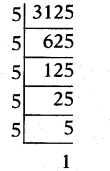
[!! Denominator is of the form 2^m× 5ⁿ. Hence a terminating decimal.]
3125 = 5⁵
∴13/3125is a terminating decimal.

ii)11/12
The denominator 12 is not a factor of 11. Moreover 12 = 2²× 3.
[!! Denominator is not of the form 2^m× 5ⁿ.]
∴11/12 is a non terminating, repeating decimal.

iii) 64/455

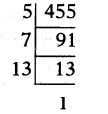
[!! Denominator is not of the form 2^m× 5ⁿ. Hence a non terminating decimal.]
∴ 455 = 5 × 7 × 13
Hence 64/455 is a non terminating, repeating decimal.

iv) 15/1600

∴ 1600 = 2⁶× 5²[∵ The denominator is of the form 2ⁿ. 5^m]
Hence 15/1600 is a terminating decimal.

v) 29/343

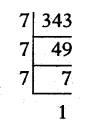
343 = 7³[Not of the form 2ⁿ. 5^m]
∴29343is a non terminating, repeating decimal.

vi)23/2³.5²
23/2³.5²is a terminating decimal.
[∵ The denominator is of the form 2ⁿ. 5^m]

vii)129/2².5⁷.7⁵
129/2².5⁷.7⁵is a non terminating, repeating decimal.

viii)9/15
9/15=3/5
Denominator is of the form 2ⁿ. 5^m.
∴915=35is a terminating decimal.

ix)36100
100 = 2²× 5²is of the form 2ⁿ. 5^m
Hence36/100is a terminating decimal.

x) 77/210

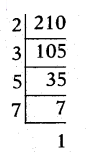
210 = 2 × 3 × 5 × 7 is not of the form 2ⁿ. 5^m
Given fraction has a non-terminating, repeating decimal expansion.

Question 3.
Write the following rationals in decimal form using Theorem 1.4.

• i)1325
• ii)1516
• iii)23/2³.5²
• iv)7218/3².5²
• v)143/110

Answer:
i)13/25

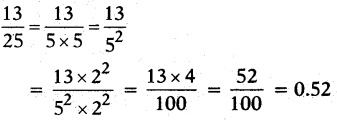
ii) 15/16
15/16 = 152×2×2×2

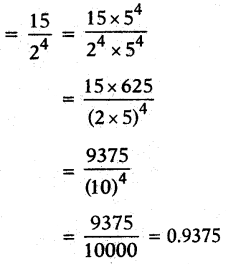
iii) 23/2³?5²

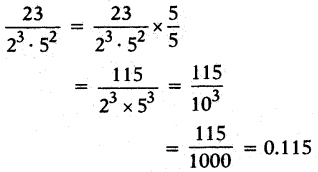
iv) 7218/3²?5²

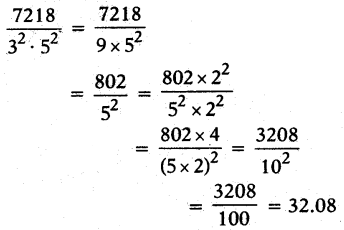
v) 143/110

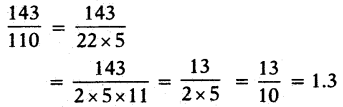
Question 4.
The decimal form of some real numbers are given below. In each case, decide whether the number is rational or not. If it is rational, and expressed in form p/q, what can you say about the prime factors of q?

i) 43.12345678?
ii) 0.120120012000120000 ……….

Question 1.
Prove that the following are irrational,

i)1/√2
ii) √3 + √5
iii) 6 + √2
iv) √5
v) 3 + 2√5

Answer:
i)1/√2
On the contrary, suppose that is a 1/√2 rational number;
then 1/√2 is of the form wherepqand q are integers.
∴ 1/√2 = p/q
⇒ √2/1 =q/p
(i.e.,) √2 is a rational number and it is a contradiction. This contradiction arised due to our supposition that 1/√2 is a rational number.
Hence 1/√2 is an irrational number.

ii) Suppose √3 + √5 is not an irrational number.
Then √3 + √5 must be a rational number.
√3 + √5 = p/q, q ≠ 0 and p, q ∈ Z
Squaring on both sides

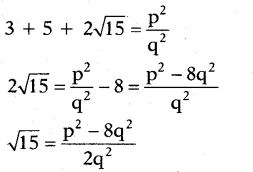
but √15 is an irrational number.
p²?8q²/2q² is a rational number
(p² - 8q², 2q² ∈ Z, 2q² ≠ 0)
but an irrational number cant be equal to a rational number, so our supposition that √3 + √5 is not an irrational number is false.
∴ √3 + √5 is an irrational number.

iii) 6 + √2
To prove: 6 + √2 is an irrational number.
Let us suppose that 6 + √2 is a rational number.
∴ 6 + √2 = p/q, q ≠ 0
⇒ √2 = p/q - 6
⇒ √2 = Difference of two rational numbers
⇒ √2 = rational number But this contradicts the fact that √2 is an irrational number.
∴ Our supposition is wrong.
Hence the given statement is true.
6 + √2 is an irrational number.

iv) √5
To prove: √5 is an irrational number.
On the contrary, let us assume that √5 is a rational number.
∴ √5 = p/q, q ≠ 0
If p, q have a common factor, on cancelling the common factor let it be
reduces to a/b where a, b are co-primes.
Now √5 =a/b, where HCF (a, b) = 1
Squaring on both sides we get
⇒ (√5)²=(a/b)2
⇒ 5 =a²/b²
⇒ 5b²= a²
⇒ 5 divides a²and thereby 5 divides 5
Now, take a = 5c
then, a²= 25c²
i.e., 5b²= 25c²
⇒ b²= 5c²
⇒ 5 divides b²and thereby b.
⇒ 5 divides both b and a.
This contradicts that a and b are co-primes.
This contradiction arised due to our assumption that √5 is a rational number.
Hence our assumption is wrong and the given statement is true, i.e., √5 is an irrational number,

v) 3 + 2√5
To Prove: 3 + 2√5 is an irrational.
On the contrary, let us assume that 3 + 2√5 is a rational number.

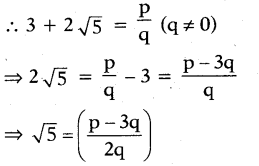
Here p, q being integers we can say that p-3q/2q is a rational number.
This contradicts the fact that √5 is an irrational number. This is due to our assumption “3 + 2√5 is a rational number”.
Hence our assumption is wrong.
∴ 3 + 2√5 is an irrational number.

Question 2.
Prove that √p + √q is an irrational, where p, q are primes.

Answer:
Given that p, q are primes.
Hence fp and fq are irrationals.
[∵ p, q have no factors other than 1 ∵ they are primes.]
Now √p + √q = sum of two irrational numbers = an irrational number
Hence proved.

Question 1.
Determine the values of the following,

i) log₂₅5
Answer:

ii) log₈₁3
Answer:

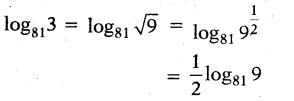
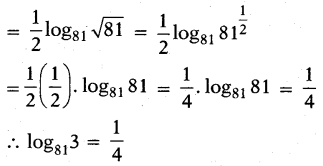
iii) log₂(1 1/6)
Answer:

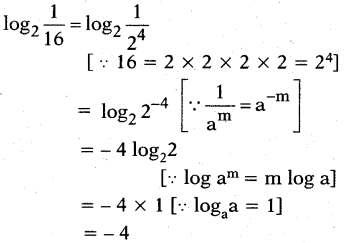
iv) log₇1
Answer:
log₇1 = log₇7⁰= 0 log₇7 = 0

v) log_x√x
Answer:

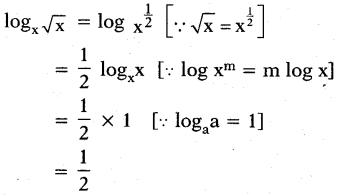
vi) log₂512
Answer:
log₂512 = log₂2⁹ [∵ 512 = 2⁹]
= 9log₂2[∵ log x^m= m log x]
= 9 × 1 [∵ log_aa = 1]
= 9

vii) log₁₀0.01
Answer:

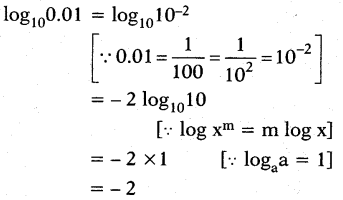
viii)log 2/3(8/27)
Answer:

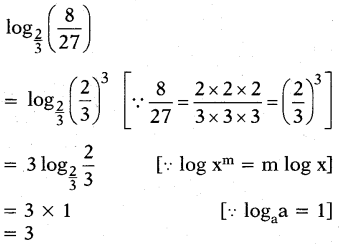
ix)2²+log₂3
Answer:
2²+log₂3= 2².2^log₂ 3[∵ a^m. aⁿ= a^m+n]
= 4 × 3 [∵log_aN= N]
= 12

Question 2.
Write the following expressions as log N and find their values.

i) log 2 + log 5
Answer:
log 2 + log 5
= log 2 × 5 [∵ log m + log n = log mn]
= log 10
= 1

ii) log₂16 - log₂2
Answer:

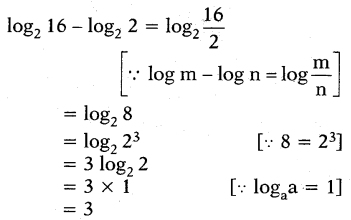
iii) 3 log₆₄4
Answer:

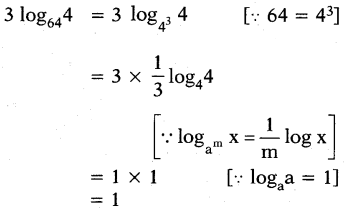
iv) 2 log 3 - 3 log 2
Answer:
2 log 3 - 3 log 2
= log 3² log 2³
= log 9 - log 8
= log 9/8

v) log 10 + 2 log 3 - log 2
Answer:
log 10 + 2 log 3 - log 2
= log 10 + log 3² log 2
= log 10 + log 9 - log 2 [∵ m log a = log a^m]
= log 10×9/2 [∵ log a + log b = log ab; log a - log b = log a/b]
= log 45

Question 3.
Evaluate each of the following in terms of x and y, if it is given x = log₂3 and y = log₂5.

i) log₂15
Answer:
log₂15 = log₂3 × 5
= log₂3 + log₂5[∵ log mn = log m + log n]
= x + y

ii) log₂7.5
Answer:

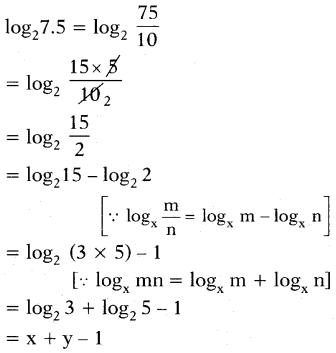
iii) log₂60
Answer:
log₂60 = log₂2²× 3 × 5
= log₂2²+ log₂3 + log₂5
= 2 log₂2 + x + y
= 2 + x + y

iv) log₂6750
Answer:

log₂6750
= log₂2 × 3³× 5³
= log₂2 + log₂33 + log₂5³
= 1 + 3 log₂3 + 3 log₂5
= 1 + 3x + 3y

Question 4.
Expand the following,

i) log 1000
Answer:
log 1000 = log 10³
= 3 log 10
= 3 × 1
= 3

ii)log[128/625]
Answer:

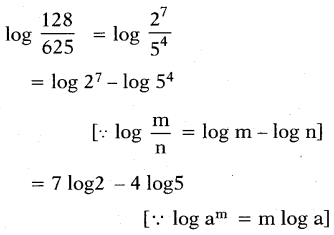
iii) log x²y³z⁴
Answer:
log x²y³z⁴= logx²+ logy³+ logz⁴[∵ log ab = log a + log b]
= 2 log x + 3 log y + 4 log z
[∵ log a^m= m log a]

iv)log p²q³/r
Answer:

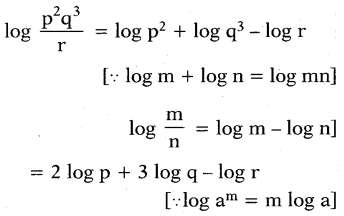
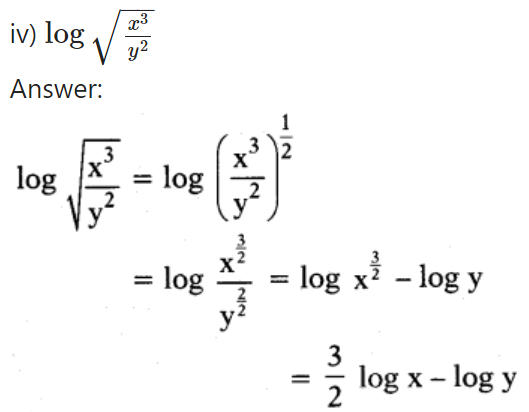
Question 5.
If x²+ y²= 25xy, then prove that 2 log (x + y) = 3log3 + logx + logy.

Answer:
Given: x²+ y²= 25xy
We know that (x + y)²= x²+ y²+ 2xy
= 25xy + 2xy [∵ x²+ y²= 25xy given]
(x + y)²= 27xy
Taking ‘log’ on both sides
log (x + y)²= log 27xy
2 log (x + y) = log 27 + log x + log y
= log 3³+ log x + log y
⇒ 2 log (x + y) = 3log3 + log x + log y

Question 6.
If log (x+y/3)=1/2(log x + log y), then find the value of x/y + y/x.

Answer:

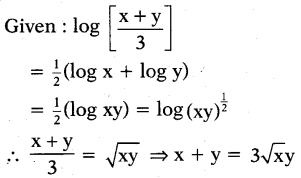
(squaring on both sides)
⇒ (x + y)²= (3√xy)²
⇒ x²+ y²+ 2xy = 9xy
⇒x²+ y²= 9xy - 2xy = 7xy

Question 7.
If (2.3)^x= (0.23)^y= 1000 then find the value of 1/x - 1/y.

Answer:
Given (2.3)^x = (0.23)^y= 1000 = 10³

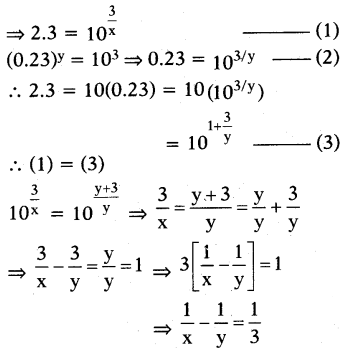
Question 8.
If 2^x+1= 3^1-xthen find the value of x.

Answer:
Given: 2^x+1= 3^1-x
log 2^x+1= log 3^1-x
(x + 1) log 2 = (1 - x) log 3
x log 2 + log 2 = log 3 - x log 3
x log 2 + x log 3 = log 3 - log 2
x (log 3 + log 2) = log 3 - log 2

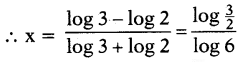
Question 9.
Is i) log 2 is rational or irrational? Justify your answer.

Answer:
Let log₁₀2 = x
Then 10^x= 2
But 2 can’t be written as 10^xfor any value of x
∴ log 2 is irrational.

ii) log 100 is rational or irrational? Justify your answer.
Answer:
Let log₁₀100 = x
⇒ log₁₀10²= x
⇒ 2 log₁₀10 = x = 2
∴ log 100 is rational.
∴ log 100 = 2
Hence rational.